Алгоритм бинарного поиска на Golang
Решил я немного освежить память по алгоритмам, потыкать их руками да заодно написать пару полезных (в первую очередь для самого себя) статеек. Да, полезно не только прочитать и сделать, но и описать процесс, так мозги лучше запоминают. Итак, эта статья положит начало циклу работы с алгоритмами!
Для языка реализации я выбрал Go, т.к. сейчас больше работаю с ним, чем с Java. И это получилось довольно интересно в силу некоторых особенностей языка, поэтому помимо алгоритма мы рассмотрим еще и их.
Немного теории
Об алгоритмах
Раз уж это первая статья на тему алгоритмов, то стоит ответить на самый главный вопрос — что такое «алгоритм» вообще. Обратимся к Википедии, как к самому «достоверному» источнику:
Алгори́тм (лат. algorithmi — от имени среднеазиатского математика Аль-Хорезми) — конечная совокупность точно заданных правил решения некоторого класса задач или набор инструкций, описывающих порядок действий исполнителя для решения определённой задачи.
В описании есть одна неточность, т.к. формулировка довольно старая — слово «порядок действий» здесь не совсем применимо, ибо алгоритмы бывают еще и разветвленные, рекурсивные и так далее, то есть это уже не совсем линейный порядок. Но тем не менее оно описывает суть — это последовательность или группа последовательностей действий, приводящих к наиболее эффективному решению поставленной задачи.
«Бинарный поиск» является самым первым приходящим на ум алгоритмом, когда встает такой вопрос в контексте программирования. Скорее всего, его спросят на собеседовании или первым начнут рассматривать на каких-нибудь курсах по кодингу на любом из языков.
Как работает бинарный поиск
Когда заходит речь про поиск чего либо в массиве данных, первым делом хочется просто пройтись по всем элементам и сравнить значение каждого с искомым. Такой путь имеет место быть, но он долгий. Не так, ОЧЕНЬ долгий. Например, если у вас будет массив из нескольких миллиардов строк, то искать значение, скрывающееся в последней строке (в самом конце массива) может быть неоправданно долго. Да и жалко столько времени тратить на перебор всех элементов.
Здесь стоит сказать про сложность алгоритмов. Подробнее про нее можно прочитать в соответствующей статье, а пока просто примем на веру, что сплошной перебор — это очень долго, а наша задача сократить это время до приемлемого.
Как это можно сделать? Сначала давайте рассмотрим, что такое массив данных. Снова обратимся к Википедии, раз уж начали с самого начала идти этим путем.
Массив — структура данных, хранящая набор значений (элементов массива), идентифицируемых по индексу или набору индексов, принимающих целые (или приводимые к целым) значения из некоторого заданного непрерывного диапазона.
Говоря простым языком, это последовательность данных какого-либо формата, элементы которой расположены друг за другом и имеют соответствующих индекс. Например, так:

Более подробно эту структуру данных я тоже хочу рассмотреть в другой статье, а пока что для наших целей хватит и такого простого описания. Внимательно посмотрим на картинку — все элементы имеют два значения:
- верхнее — индекс элемента в массиве;
- нижнее — условные данные, хранящиеся в ячейке массива.
Здесь важен нюанс: индексы элементов всегда будут оставаться в последовательном порядке, тогда как данные в каждой ячейке могут лежать совершенно разные, и не обязательно в порядке возрастания.
Представим массив из 10 ячеек, как на рисунке выше. Чтобы перебрать все его элементы с 1 по 10 и сравнить с данными, которые мы ищем, придется выполнить 10 сравнений. Да, возможно и меньше, если искомый элемент будет в начале массива, но в теории алгоритмов принято исходить из самого тяжелого случая — считаем, что понадобится 10 сравнений.
Но ведь получается, что мы выполним просто целую кучу ненужной работы! Вот если бы можно было выбросить хотя бы половину элементов… И вот здесь вступает в силу алгоритм бинарного поиска.
Бинарный — двоичный, представленный элементами всего двух видов.
Разделим массив на две половинки, и посмотрим, в какой из них находится нужный нам элемент, сравнив его значение с тем, которое в текущий момент посередине массива. Также может оказаться, что искомое значение и есть «серединка».
Стоп! Помните, что данные в массиве могут быть в случайном порядке? Если мы сейчас начнем сравнивать элементы с серединой, то получим абракадабру, т.к. не будет никакой логики в том, где эти элементы расположены, и гарантировать положение большего элемента в правой части относительно меньшего будет уже нельзя. Отсюда вытекает главное правило бинарного поиска — он работает только с отсортированными данными!
Итак, делим массив пополам и определяем, в какой из половинок оказался тот элемент, который мы ищем. Для примера будем искать элемент data8 из массива на рисунке выше.

Что у нас получается? 10 / 2 = 5. Берем элемент №5 по индексу в массиве и сравниваем данные из него с data8. В пятой ячейке лежит data5, значит data8 оказывается в правой отсеченной половине массива. Мы отбросили половину массива слева, убедившись, что в ней нет элемента, который мы ищем.
Обратите внимание, что данные поделены не ровно: справа осталось пять ячеек, а слева всего четыре. Это логично вытекает из-за не возможности деления без остатка целых чисел. Поэтому может получаться так, что одна из «половин» будет больше другой. На действия алгоритма это вообще никак не влияет.
Также обратите внимание на тот факт, что мы в любом случае сравниваем значения данных в ячейках. Может возникнуть вопрос — а как же быть, если там не числа? Ответ прост: сравнить можно вообще любые данные. В Java, например, для произвольных классов объектов можно задавать параметры сравнения для встроенного и предлагаемого для каждого объекта метода equals, возвращающего результаты сравнения двух объектов заданного класса.
Что делать дальше? Повторяем процедуру. За основу берем правый кусок и делим его пополам:
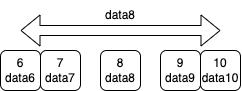
Мы снова поделили диапазон пополам и начали сравнивать: о чудо, data8 оказался прямо по центру, то есть при сравнении оказалось, что мы нашли элемент. На этом алгоритм может завершаться, вернув нам значение 8 как индекс элемента, который мы ищем.
Решением всегда будет именно «средний» вариант. Все зависит от количества элементов в остатке — если осталось два элемента, то, условно, «средним» станет один из них, и либо он и есть решение, либо второй.
Здесь для упрощения был взят такой пример, чтобы на втором шаге «попасть» на нужный элемент. В реальности же все может дойти до того, что останется всего один элемент из всего огромного массива. Но неоспоримым является тот факт, что для нахождения элемента нужно гораздо меньше времени и трудозатрат, чем при переборе всех элементов массива с первого по последний.
Давайте напишем код бинарного поиска.
Реализация алгоритма на Go
Я считаю, что написать только функцию, осуществляющую поиск элемента в массиве, будет не совсем правильно, т.к. не получится ее запустить и убедиться, что все работает как нужно. Поэтому помимо самого поиска я предлагаю написать еще и минимальную обвеску, добавляющую интерактивности нашей программе. Создадим новый файл *.go с функцией main() и добавим туда следующий код:
func main() {
var elems, lookingFor int
fmt.Print("Number of elements? ")
fmt.Scan(&elems)
var array = make([]int, elems)
fmt.Print("Generated array: ")
for i := 0; i < elems; i++ {
array[i] = i
fmt.Print(strconv.Itoa(i) + " ")
}
fmt.Println()
fmt.Println("What are we looking for:")
fmt.Scan(&lookingFor)
}
Здесь мы сделали следующее:
- Создали две переменных:
elems— количество элементов в массиве, в котором мы будем искать;lookingFor— число, которое будем искать.
- Попросили пользователя ввести с клавиатуры количество элементов в массиве и записали это число в объявленную ранее переменную.
- Создали новый массив, состоящий из заданного пользователем количества элементов.
- Заполнили созданный массив числами по порядку (массив же нужен отсортированный);
- Запросили у пользователя число, которое будем искать и сохранили его в нужной переменной.
Теперь нужно реализовать функцию бинарного поиска. Тут наступает тот самый момент, который я упоминал ранее. А что делать, если мы ничего не нашли, то есть элемента нет в массиве? В Java я бы просто вернул Null, проверил на него ответ и все. Но Go не позволяет функции вернуть nil (Go’шный аналог Null), если у нее заданы четкие параметры возврата.
Выход есть, и кроется он в особенности Go, которая заключается в том, что в этом языке функция может возвращать не одно, а целых два значения. Просто вернем помимо ответа еще и булевый результат поиска — true или false. Давайте набросаем функцию поиска:
func binarySearch(array *[]int, lookingFor int) (int, bool) {
fmt.Println("Looking for...")
var mid, assumption int
min := 0
high := len(*array) - 1
for min <= high {
mid = (min + high) / 2
assumption = mid
if assumption == lookingFor {
return assumption, true
}
if assumption > lookingFor {
high = mid - 1
} else {
min = mid + 1
}
}
return 0, false
}
Функция binarySearch принимает на вход два параметра:
array *[]int— указатель на массив, в котором будем искать (можно считать, что просто массив, без указателя, если вы с ними ранее не сталкивались);lookingFor int— число, которое нужно найти.
Возвращать же она будет два параметра: (int, bool), где первое — найденные данные, а второе — булевый флаг успешности поиска. В принципе, здесь можно возвращать и индекс элемента массива, если стоит задача убедиться в наличии данных в нем. Я решил возвращать сами данные.
В начале функции мы задали две переменных: mid и assumption. По названию можно догадаться, что первая — это индекс среднего элемента, а вторая — найденное число (при условии, что оно есть в массиве). Давайте посмотрим на алгоритм функции, чтобы лучше понять, как она работает:
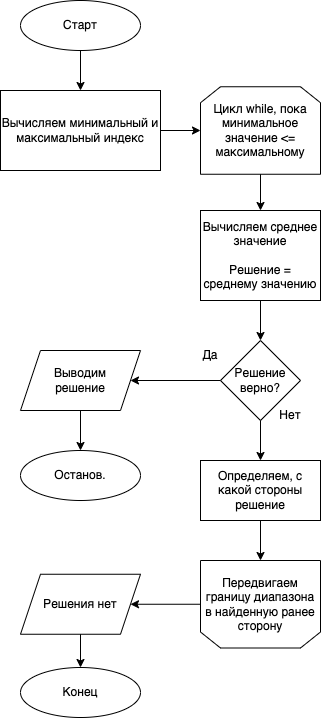
Здесь стоит обратить внимание только на два момента.
Первый — цикл for min <= high, который может вызвать недоумение, если вы пришли сюда не с Go. По сути это обычный while, просто в Go он делается через for.
Второй: момент, когда мы двигаем диапазоны. Оно вроде бы понятно сразу из кода, но на всякий случай поясню:
- если искомое число слева от середины, то сдвигаем правую границу на 1 налево от среднего значения;
- если справа — сдвигаем левую границу направо на 1 от середины.
Давайте посмотрим на весь код целиком, а затем приступим к тестам:
package main
import (
"fmt"
"strconv"
)
func main() {
var elems, lookingFor int
fmt.Print("Number of elements? ")
fmt.Scan(&elems)
var array = make([]int, elems)
fmt.Print("Generated array: ")
for i := 0; i < elems; i++ {
array[i] = i
fmt.Print(strconv.Itoa(i) + " ")
}
fmt.Println()
fmt.Println("What are we looking for:")
fmt.Scan(&lookingFor)
var assumption, result = binarySearch(&array, lookingFor)
if result {
fmt.Println("Found: " + strconv.Itoa(assumption))
} else {
fmt.Println("Nothing found!")
}
}
func binarySearch(array *[]int, lookingFor int) (int, bool) {
fmt.Println("Looking for...")
var mid, assumption int
min := 0
high := len(*array) - 1
for min <= high {
mid = (min + high) / 2
assumption = mid
if assumption == lookingFor {
return assumption, true
}
if assumption > lookingFor {
high = mid - 1
} else {
min = mid + 1
}
}
return 0, false
}
Исходные коды программы и рисунков (в формате drawio) можно найти в репозитории.
Тестирование программы
Давайте запустим получившуюся программу и проверим, что все работает как нужно. Можно задать любые диапазоны и числа, но я предлагаю сделать так же, как и в примере выше:
$ go run main.go
Number of elements? 10
Generated array: 0 1 2 3 4 5 6 7 8 9
What are we looking for:
8
Looking for...
Found: 8
Я для красоты добавил еще вывод всего массива, чтобы было видно более наглядно, как все работает… и работает ли. Попробуем найти элемент, находящийся в левой половинке массива:
$ go run main.go
Number of elements? 10
Generated array: 0 1 2 3 4 5 6 7 8 9
What are we looking for:
3
Looking for...
Found: 3
Отлично! Теперь последний шаг: поиск элемента, выходящего за границы массива:
$ go run main.go
Number of elements? 10
Generated array: 0 1 2 3 4 5 6 7 8 9
What are we looking for:
11
Looking for...
Nothing found!
Все работает как и ожидалось.
Заключение
Мы рассмотрели пример реализации бинарного поиска на языке Go с подробным разбором самого алгоритма. Надеюсь, это кому-то будет полезно (мне так точно было!).